动态规划算法，分别用C语言，C++,java,python编写出来

源码资源网

很多人都会觉得动态规划很难，动态规划的核心思想有以下两点：

第一，任何看似很复杂很难解决的问题，其实都可以归结为一系列子问题，无论一个问题有多复杂，只要他有解决方案，就可以归结为N个子问题，某种意义上，我们可以认为动态规划是对递归的一种优化；

第二，我们在解决N个子问题的时候，要留心整体上有没有做无用功，通过备忘录的方式保存中间状态，使得不反复去计算已经求得的中间解。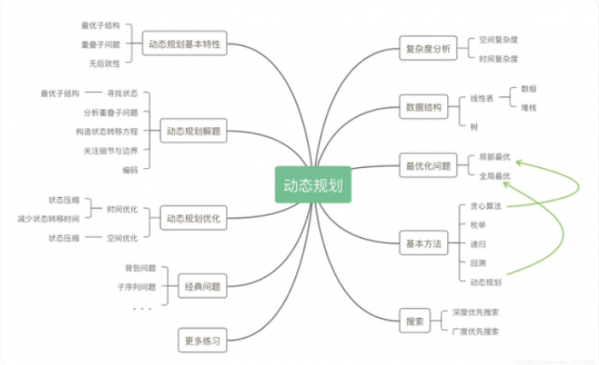

动态规划算法，分别用C语言，C++,java,python编写出来
当涉及动态规划算法时，可以使用多种编程语言来实现。以下是使用C语言、C++、Java和Python编写动态规划算法的示例：
1.**C语言示例：**

1. #include <stdio.h>
   
2. int fibonacci(int n) {
   
3.     int dp[n+1];
   
4.     dp[0] = 0;
   
5.     dp[1] = 1;
   
6.      for (int i = 2; i <= n; i++) {
   
7.         dp[i] = dp[i-1] + dp[i-2];
   
8.     }
   
9.      return dp[n];
   
10. }
    
11. 
    

复制代码

游客，本帖隐藏的内容需要积分高于 9 才可浏览，您当前积分为 0

2.**C++示例：**

1. #include <iostream>
   
2. using namespace std;
   
3. int fibonacci(int n) {
   
4.     int dp[n+1];
   
5.     dp[0] = 0;
   
6.     dp[1] = 1;
   
7.      for (int i = 2; i <= n; i++) {
   
8.         dp[i] = dp[i-1] + dp[i-2];
   
9.     }
   
10.      return dp[n];
    
11. }
    
12. 
    

复制代码

游客，本帖隐藏的内容需要积分高于 9 才可浏览，您当前积分为 0

3.**Java示例：**

1. public class Fibonacci {
   
2.     public static int fibonacci(int n) {
   
3.         int[] dp = new int[n+1];
   
4.         dp[0] = 0;
   
5.         dp[1] = 1;
   
6.          for (int i = 2; i <= n; i++) {
   
7.             dp[i] = dp[i-1] + dp[i-2];
   
8.         }
   
9.          return dp[n];
   
10.     }
    
11.    
    
12. }

复制代码

游客，本帖隐藏的内容需要积分高于 9 才可浏览，您当前积分为 0

4.**Python示例：**

1. def fibonacci(n):
   
2.     dp = [0] * (n+1)
   
3.     dp[0] = 0
   
4.     dp[1] = 1
   
5.      for i in range(2, n+1):
   
6.         dp[i] = dp[i-1] + dp[i-2]
   
7.      return dp[n]
   
8. 
   

复制代码

游客，本帖隐藏的内容需要积分高于 9 才可浏览，您当前积分为 0

这些示例展示了使用不同编程语言实现斐波那契数列的动态规划算法。您可以根据需要修改算法和输入值。请注意，这只是动态规划算法的简单示例，实际应用中可能会有更复杂的问题和算法。


扫码关注微信公众号，免费查看完整算法内容。